تاریخچه مختصری از هندسه
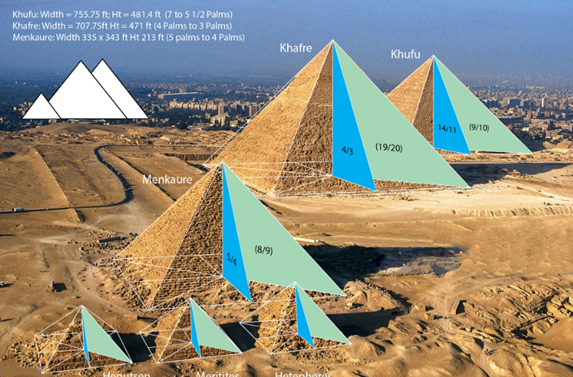
شاید جمله هندسه از مصر آغاز شد سخن گزافی نبوده باشد. پیش از پیدایش فیلسوفان مهندس یونان، انها هندسه ای را آموخته بودند که آنها را بر تارک تاریخ هندسه جلوه گر می سازد. بقول هرودوت هندسه آنها از روی ضرورت بود.
هر سال که نیل طغیان می کرد تمام مرزبندی های زمین های حاصلخیز کنار نیل از بین می رفت و مسائل اقتصادی از قبیل پرداخت مالیات ایجاب می کرد که ایشان از روشی برای پیاده سازی دوباره حدود زمین هایشان استفاده کنند تا نرخ مالیات هایشان به صورت ثابت باشد و همچنین املاک خود را بشناسند و حدود آن را برای سالیان حفظ کنند.
شیوه ریاضیات کاربردی آنها هم بر اساس ریاضیات پایه ای و ساده ای استوار بود. بدین صورت که از تیر و طناب برای اندازه گیری استفاده می کردن. طنابی که احتمالا 12 چوب به ان در فواصل یکسانی متصل بوده و با استفاده از سه چوب در یک بعد و ادامه چهار چوب در بعد دیگر حدود زمین ها را مشخص و زاویه دقیقی که اکنون ما می دانیم که نود درجه بوده است را مشخص می کردند.
آنها نیاز به دقت و سرعت در اندازه گیری و پیاده سازی حدود بودند. این گونه محاسبات هندسی ایشان تاثیر بسیاری بر همسایگان شمالی انها که یونانیان بودند گذاشت به طوریکه اگر اشنا باشید فیثاغورث همین تکنیک مصریان را با نام قضیه فیثاغورث استدلال استنتاجی کرده و به اثبات مستدل ریاضی رساند که هم اکنون نیز ما در کاربردهای فراوانی از ان استفاده می کنیم.
اما هندسه در یونان به شکوفایی رسید و یونانیان عموما فیلسوف از روش های استدلالی استنتاجی گزاره های فراوان هندسی را یافته و آنها را توسعه دادند.

ویرانه های باقی مانده از یونان باستان. یونانیان پیشرفته ترین هندسه دوران باستان را دارا بودند. طراحی معابد آنها تبلور احساس زیبایی شناسی این مردمان باستان است.
هندسه مصریان و بین النهرینیان بسیار مختصر و کم محاسبه بود اما وقتی به یونان رسید توسعه داده شد و بررسی های فراوانی بر روی هر یک از اوبزه های هندسی صورت گرفت.
آنها نه بر این پرداختند که چه چیزی از هندسه عایدمان می شود بلکه این سوال را داشتند که چگونه می شود و این سرآغاز استدلالهای استنتاجی منطقی بر روی اوبژکت های هندسی بود که مسیر را برای علم هندسه بشری تعیین کرد. این مسیر با دانشمند بزرگی چون تالس شروع می شود.

تالس (624 قبل از میلاد)
تالس شروعی بر هندسه
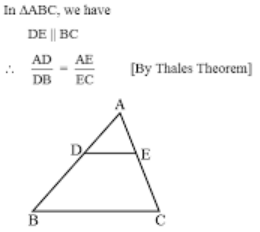
تالس فراتر از یک فیلسوف یا ریاضیدان بود. او بر سر خط ریاضیدانان یونان ایستاده است. همچنین او یک تاجر نیز بود. هنگامیکه محصول زیتون رشد زیادی کرد تمام زیتون منطقه زندگی خود را خرید و مانع از ایجاد فروش انحصاری توسط دیگران شد و در زمان لازم به قیمت منصفانه ای ان را فروخت. او بسیار سفر می کرد و آموخته های اولیه وی از هندسه نیز به همان زمان بر می گردد. قضیه معروف وی را در تصویر زیر می بینید.
ادامه راه تالس با فیثاغورس
شاگرد تالس که فیثاغورس نام دارد نیز یکی از معلومات هندسی پیشین را با استدلال استنتاجی به اثبات رساند که اکنون به قضیه فیثاغورث معروف است. برخلاف تالس که بیشتر یک تاجر بود فیثاغورث یک عارف بود و علاقه وافر و بی حد و حصری به اعداد و ریاضیات داشت. علاقه او بیشتر از هندسه به اعداد بود زیرا که فردی مذهبی بود، بخصوص اعداد خاصی که در پایتا گورا که از علایق مذهبی وی بود.
او نیز همانند تالس سفر بسیار می کرد. بعد از اینکه سفرهایش را به اتمام رساند فرقه ای شکل داد و به اکتشاف ریاضیات می پرداختند و هیچکس با کشف ریاضی که می کرد برای خویش اعتباری نمی خواست.
به عنوان یک نتیجه ، ما نمی توانیم بدانیم که فیثاغورس چه چیزی را کشف کرده و کار پیروان وی چه بوده است. با این حال می توانیم اطمینان داشته باشیم که او اولین کسی نبود که قضیه فیثاغورس را کشف کرد. ما قبلاً دیده ایم که قضیه ای که نام فیثاغورس را به خود گرفته است بیش از هزار سال قبل از تولد فیثاغورس توسط بین النهرینیان شناخته شده و مورد استفاده گسترده قرار گرفته است.
برخی می گویند او اولین کسی بود که قضیه را اثبات کرد. شاید او بود ، اما هیچ مدرکی برای تأیید این ادعا در دست نیست. هیچ کدام از اینها از اهمیت وی در تاریخ ریاضیات کم نمی کند.
یونانیان هندسه را به پارادایم قیاس و استدلال بردند و تاکید خود را از حوزه شهود برداشتند و بر این نحل عمل کردند و این شد که ریاضیات به صورت یک علم زیبا و تغییر ناپذیر درآمد که عموم پدیده ها را می توانست بیان کند.
نسبت های طلایی نیط منتسب به فیثاغورسیان است. نسبت طلایی یک نسبت خاص است که یونانیان آن را به عنوان نسبت بین دو بخش خط نشان می دهند. یک راه ساده برای نشاان دادن نسبت طلایی فرض کردن یک پنتاگون ستاره ای است.
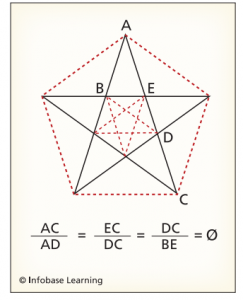
این شکل یک ماهیت خود تکثیری (Self-Propagating) دارد بدین صورت که در داخل هر ستاره یک پنتاگون است و در هر پنتاگونی یک ستاره (اندکی بیشتر بیاندیشید!)
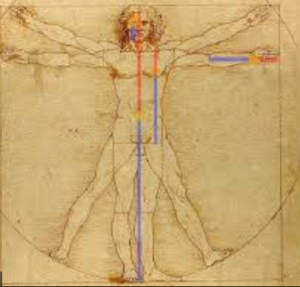
ما این نسبت های زیبا را و چشم نواز را در صنایع دست انسان (معماری یونانیان) و طبیعت (برخی از تناسبات بدن انسان) می توانیم ببینیم. اهمیت این کشف برای فیثاغورث و شاگردانش به حدی بود که آن را نماد گروه خود ساخته بودند.
هر چند که ایشان آن را انحصاری نکردند و از اینرو هنرمندان و معماران فراوانی از این یافته ها در طراحی های خود استفاده کردند. نسبت های طلایی به تناوب در نقاشی های غربی تا اوایل قرن بیستم به کار گرفته شده اند و همانطور که گفتیم نکته شگفت انگیز اینکه این نسبت ها در طبیعت نیز ظاهر می شوند. جالب است که بدانید که یکی از اصلی ترین روش هایی که ویلیام دلبرت گن در روش های خود از آن بهره میبرد ، هندسه بود.
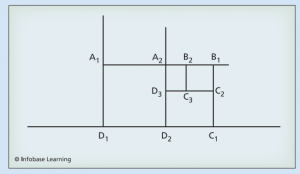
عدد فی
بعضی اوقات راحت است که نسبت طلایی را با یک عدد نشان دهید. نسبت طول هایی که بخش طلایی را تعیین می کنند عددی را تعیین می کنند که غالباً با حرف یونانی φ یا phi تلفظ مشخص می شود. این یک عدد غیر گویا (گنگ) است که تقریبا برابر با 1.618 است.
اندازه هایی که در طبیعت وجود دارد که φ را می توان در آن یافت
1-در بدن یک فرد بالغ نسبت قد به میزان از ناف به بالا تقریب خوبی در مورد نسبت طلایی می زند.
2-توزیع برگ ، ساقه و بذر در گیاهان غالباً به گونه ای است که نسبت طلایی حاصل می شود.

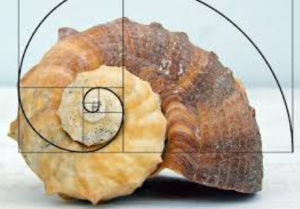
3-منحنی به نام مارپیچ لگاریتمی شکل که در بسیاری از شاخ های حیوانات و پوسته های مارپیچی یافت شده است.
فرزاد شیبانی


