هندسه در گذر زمان

در ادامه مقاله تاریخچه ی هندسه به ارائه تاریخچه ای بیشتر از هندسه میپردازیم:
همانطور که در مقاله پیشین دیدید به خاستگاه هندسه و علت پیدایش ان پرداختیم و مرحله رشد و نمو آن را نیز دیدیم. اهمیت هندسه برای یونیان به حدی بود که به عنوان یک مطلب عمومی غالب افراد جامعه باید به آن اگاه می بودند. هندسه راه بسیاری را بر روی بشر گشود. هر انچه که قابلیت تجسم پیدا می کرد بواسطه هندسه استدلال و استنتاج شده و مجهولات پیدا می شد و به همین روال مسائل جدیدتری که رخ می نمود. طراحی و احداث راه های مناسب، ترسیم و ساخت شهرها و کلانشهرهای مهندسی شده، تاسیسات زیربنایی بهینه شده، طراحی و ساخت ابزارهای کارآمدتر و … نمونه های بسیاری از فواید هندسه برای بشریت می باشند.
همانطور که در مقالات پیشین (مقایسه فیزیک نیوتن و انیشتین ) دیده اید، اصولا نگاه و شیوه نگرش دکارت به پیرامون از بعد عمومی خارج بود و این نوع نگاه منجر به انقلابات فکری در تاریخ علم و فلسفه شده است که نیوتن یک نمونه از اینهاست.

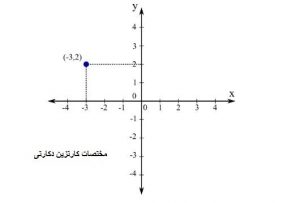
در مورد هندسه نیز نگاه دکارت به جبر و هندسه و به طور کلی ریاضیات منجر به تولید دستگاه مختصاتی شد که اکنون به عنوان دستگاه مختصات دکارتی آن را می شناسیم. دکارت به منظر دید اهمیت بسیاری می داد و اینکه از کجا بدین مفهوم نگریسته می شود ابعاد بسیار عمیقی را در اندیشه وی داشت.
با ورود جبر به هندسه گسترش هندسه به دامنه های دیگری انجامید و باعث توسعه بخش هایی از هندسه شد که قبلا از ان شناخته نشده بود و با تلاش ها و مطالعات دانشمندان گرانقدری همچون گاوس و اویلر و دیگر نوابغ جبر و هندسه علومی ریاضیاتی همچون حساب دیفرانسیل و توپولوژی بنیان نهاده شد که با گسترش این علوم تمدن بشری استفاده ای بسیار زیادی را توانست از طبیعت و پیرامون خود انجام دهد یا اینکه نحوه استفاده خود را بهینه کند. البته به نحوی این رشد ریاضیات را باید به کلیسا نسبت داد زیرا که کلیسا هیچ گونه نظر انتقادی در مورد مسائل فیزیک را که بنحوی اصول گفته شده توسط مسیحیت را از متزلزل سازد نمی پذیرفت و این موضوع باعث توجه هر چه بیشتر دانشمندان به هندسه و ریاضیات شده بود.

همانطور که احتمالا شنیده اید هندسه ای به نام هندسه نااقلیدسی وارد مطالب مطروحه ریاضیات و هندسه شده است اما خاستگاه ان چیست؟
در اصل هندسه ای که ما در کتاب های اولیه از هندسه با ان آشنا شده ایم همان هندسه اقلیدسی است که به پاس گرامیداشت این مرد بزرگ دوران باستان نامگذاری شده است اما این هندسه جدید چیست؟ بگذارید اندکی شما را با هندسه نااقلیدسی آشنا کنم.
فرض کنید شما بر روی یک کاغذ دو خط موازی را ترسیم کنید، آیا این دو خط به یکدیگر خواهند رسید؟ جواب این سوال در نگاه اول نرسیدن است اما اگر به این موضوع عمیقتر نگاه کنیم به جواب متفاوتی خواهیم رسید که بنیان های هندسه نااقلیدسی را شکل می دهد. وقتی شما بر روی یک کاغذ دو خط موازی ترسیم می کنید از انجا که بر روی زمین کروی استاده اید و آنرا رسم می کنید به طور قطع این دو خط در بی نهایت به همدیگر خواهند رسید. البته گونه دیگری از هندسه نااقلیدسی وجود دارد که می گوید این دو خطط موازی به همدیگر مخواهد رسید. در اصل عاملیت در هندسه نا اقلیدسی با سطح یا حجمی است که پایه است و آن سطح یا حجم است که تعیین می کند دو خط به هم برسند یا خیر.
دیدید که اختلاف هندسه اقلیدسی و نااقلیدسی در کجاست؟ در اصل هندسه اقلیدسی دارای اصل مهمی بود که میگفت تنها و تنها یک خط میتوان از یک نقطه خارج خط بر خط ترسیم کرد که بر خط عمود باشد( یعنی کمترین فاصله از خط) اما همین اصل محل مناقشه ریاضیدانان قرن هفدهم شد تا مبانی اولیه هندسه نااقلیدسی را طرح ریزی کنند که بعد از ان نیز منجر به گشایش های بسیار فوق العاده ای در سایر علوم علی¬الخضوص فیزیک، مهندسی ماهواره ها، نقشه برداری و ناوبری هواپیماها و کشتی ها شدند. برخی از ملاحظات هندسه اقلیدسی با اینگونه سوالات به لرزه می افتاد و مهم آنکه قادربه پاسخگویی به سوالات مطروحه اختر شناسی و فیزیک جدید نبود اما هندسه نااقلیدسی چنین کمبود هایی را برطرف می کرد.
یکی از این افراد که از پایه گذاران هندسه نااقلیدسی است لباچفسکی است.

پس همانطور که می بینید مفاهیم در فضای هندسه اقلیدسی به سمت انتزاعیاتی می روند که با ادراک ما فاصله بیشتری می گیرند ولی همانقدر که از شهود ما فاصله می گیرند توانایی تطبیقشان با واقعیت های علمی نیز بیشتر است به طوریکه موارد پیچیدگی در فضا و زمان و امثالهم با هندسه نااقلیدسی عجین شده است.
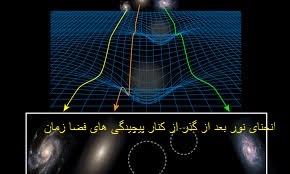
نظریه ریسمان ها نیز که تازه ترین و محیرالعقولترین نظریه در حوزه فیزیک ذرات است نیز دارای اتمسفری به غایت هندسی و نااقلیدسی است.

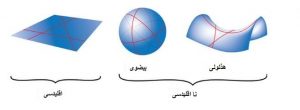
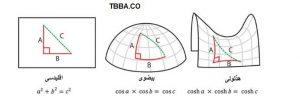
هندسه نااقلیدسی در دو حوزه هذلولی و بیضوی توسعه یافته است. اگر همان مثال دو خط موازی را دوباره در ذهن خود تصویر سازی کنید این دو خط در فضای واقعی یا از هم دور می شوند که به توسعه هذلولی هندسه نااقلیدسی مرتبط است یا به هم نزدیک می شوند تا اینکه به هم برسند و این به توزیع بیضوی هندسه نااقلیدسی بر میگردد.
فرزاد شیبانی



